Расчет магнитостатического поля

В магнитостатических задачах магнитное поле создано постоянными токами, протекающими в проводниках/катушках, и постоянными магнитами. Электрическое поле ограничено объектами, смоделированными как реальные (неидеальные) проводники. Электрическое поле, существующее в проводниках как следствие текущего постоянного тока, полностью отделено от магнитного поля. В соответствии с заданными магнитными свойствами материалов распространение магнитного поля зависит от пространственного распределения магнитной проницаемости. В магнитостатической задаче нет никаких эффектов изменения во времени, и объекты, как предполагается, являются стационарными. Энергетическое преобразование, связанное с магнитостатической задачей, - это только омические потери, связанные с токами, текущими в реальных проводниках.

Решение магнитостатической полевой задачи определяется следующими двумя уравнениями Максвелла:

кроме того, используется следующая важная зависимость:

где:

• напряженность магнитного поля.

• плотность магнитного потока.

• плотность тока проводимости.

• постоянное намагничивание.

•  магнитная проницаемость вакуума.

• относительная магнитная проницаемость.

Для нелинейных материалов зависимость между H и B поля является нелинейной и может быть изотропной или ортотропной (в случае анизотропного поведения - это тензор). Также в реальных случаях нелинейность может встречаться и учитываться и в постоянных магнитах. Кроме того, если состояние намагниченности рассматривается для (нелинейных) постоянных магнитов, работающих ниже перегиба, Maxwell предусматривает расширенные опции, позволяющие получить решение, основанное на ранее вычисленной рабочей точке намагниченности. Если нелинейность встречается в магнитомягких материалах (с незначительным гистерезисом) одновременно с ортотропным поведением, для Maxwell требуется, чтобы были заданы кривые BH по координатам в соответствующем(их) материале(ах). Из этих кривых зависимость энергии от H берется по каждой из координат и используется в процессе получения нелинейного тензора проницаемости, используемого в итерационном процессе решения Ньютона-Рафсона:

где: и - предыдущее полевое решение, - общий полный тензор, и присвоено следующее:

где учитывают анизотропные эффекты любых слоистостей материала, имеющихся в модели.

Трехмерный магнитостатический solver рассматривает магнитное поле H со следующими компонентами:

где - магнитный скалярный потенциал, - частное решение, полученное присвоением всем граням сетки значений, определяемых законом полного тока для всех контуров всех поверхностей тетраэдров в сетке, и создано постоянными магнитами. Таким образом, переменные расчета - это узловые величины магнитного скалярного потенциала (десять величин в одном четырехграннике - в каждой из четырех вершин и во всех шести серединах узловых ребер), при этом должна обеспечиваться квадратичная аппроксимация внутри каждого конечного элемента.

У этой формулировки есть большие преимущества перед возможными другими, в частности использование значительно меньшего количества вычислительных ресурсов (из-за скалярной сущности переменных). Магнитостатический solver обрабатывает линейные и нелинейные трехмерные задачи. В случае нелинейных задач используется классический итерационный алгоритм Ньютона-Рафсона с управляемой пользователем точностью.

Магнитостатический solver вычисляет распространение магнитного поля, созданного сочетанием известного распространения вектора плотности постоянного тока и пространственного распространения объектов с постоянным намагничиванием. Также можно применить граничные условия к модели таким образом, что возможно моделирование установки устройства во внешнее магнитное поле. В последнем случае граничные условия должны быть применены таким способом, чтобы уравнения Максвелла не нарушались внутри области решения или на границах.

Типичные источники для магнитостатических полевых задач - это напряжение, ток, постоянное намагничивание и плотность тока. При использовании источников в задачах магнитного поля применяемое распространение тока должно быть свободным растеканием во всей области решения, поскольку физически это квазистационарное распространение плотности тока проводимости. Таким образом, путь(и) проводимости (conduction path(s)) для применяемых распространений тока должны быть замкнуты, т.е. полностью находиться в пределах области решения задачи или начинаться и заканчиваться на границах.

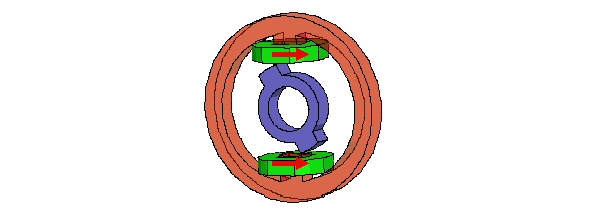
Закрытые conduction paths в двух обмотках (один источник тока применяется к terminal в каждой обмотке)

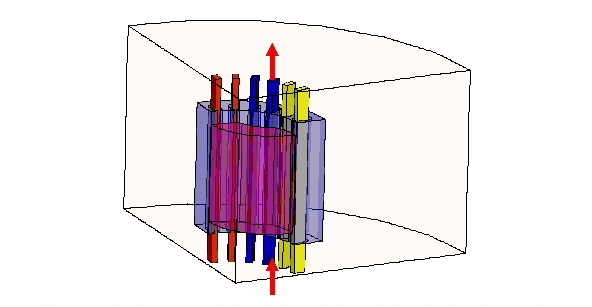
Источники тока применяются к границам на обоих концах проводников (не требуется задавать "terminals")

Полный ток для проводников, которые касаются границы, не требует наличия специальных выводов (terminals) на концах conduction path, потому что для возбуждения могут использоваться соответствующие плоские поверхности проводников, находящиеся в плоскости границ области решения. В случае закрытого conduction path должен быть создан terminal (плоский объект), т.к. в качестве возбуждения (источника тока/напряжения) используется соответствующее сечение проводника в выбранном месте.

Источники напряжения Voltage (по крайней мере, два) должны быть определены таким образом, чтобы ток мог течь в соответствующих проводниках для формирования непрерывного conduction path. Источники Voltage drop (падения напряжения) нужно использовать для закрытых conduction paths (возможно, содержащих объекты с различной электропроводностью) прежде всего в ситуациях, где полный ток неизвестен. Для одного conduction path применяется один источник voltage drop. Полный ток для любого conduction path должен быть больше нуля.

Магнитостатический solver не вычисляет распространение электрического поля, связанное с распространением напряжения за пределами проводников. Однако электрическое поле внутри проводников косвенно доступно для post processing (обработки после расчета) через распространение плотности тока проводимости. Таким образом, можно вычислить омические потери в проводниках с применяемыми источниками тока и напряжения.

Постоянное намагничивание в Maxwell ® обрабатывается, как свойство материала, но мы его здесь упоминаем, поскольку оно имеет характеристики источника.

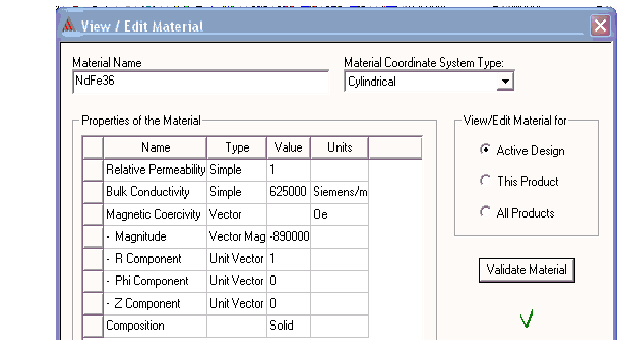
Постоянное намагничивание может быть определено в декартовых, цилиндрических или сферических системах координат материалов, как показано в вышеприведенном окне, где составляющие по R, Phi, и Z (в цилиндрической системе, которая рассматривается здесь, как пример) могут быть определены в любой реальной комбинации. Фактическое направление векторного свойства определено, когда свойство назначено на объект и когда выбрана нужная система координат (глобальная система координат существует всегда, но могут быть определены и дополнительные). В случае необходимости могут быть определены и использоваться дополнительные относительные системы координат, чтобы определить ориентацию векторного свойства.

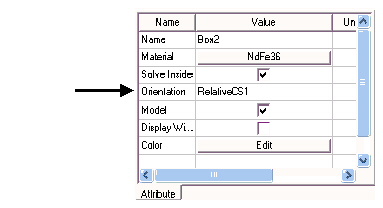
В то время как тип системы координат материала заложен в определение материала, фактическая ориентация может быть не такой, которая была определена свойством материала, например, в цилиндрической системе свойство может быть применено ко многим предметам с различными ориентациями, если были определены и использовались в процессе назначения соответствующего свойства материала несколько относительных локальных систем координат.

Типичные граничные условия, используемые в магнитостатических задачах, - это тангенциальность магнитного поля (по умолчанию - естественное граничное условие, которое автоматически применяется ко всем поверхностям области решения, т.е. к поверхностям объекта геометрии, содержащего внутри всю модель). Это граничное условие по умолчанию может быть изменено, если ко внешним поверхностям пространства решения применены другие граничные условия. Граничное условие по умолчанию ограничивает магнитное поле в пространстве решения; поэтому эта граница должна быть отнесена на некоторое расстояние от источников, чтобы избежать сверхограниченности области при размещении границы близко к объектам модели. Несмотря на то, что трудно дать "рецепты" с универсальной обоснованностью относительно размещения границ задач, хорошее эмпирическое правило утверждает, что если модель может быть представлена находящейся внутри сферы радиуса R, то границы могут быть размещены в 4-5 радиусах R от воображаемого центра модели.

Zero Tangential H Field (нулевое тангенциальное поле H) позволяет пользователю задать нормальную (в среднем) полевую ориентацию на произвольной поверхности. Это граничное условие не требует дальнейшего вмешательства пользователя, в том смысле, что никакие значения и системы координат не требуются.

В случае граничного условия Tangential H Field (тангенциальное поле Н) должны быть определены и впоследствии использоваться значения двух тангенциальных составляющих и поверхностная система координат. Это граничное условие используется только для двух типов поверхностей: плоская и цилиндрическая. Координатная система для плоскости будет прямоугольной с X и Y составляющими H в этой плоскости. Система координат для цилиндрической поверхности будет иметь ось Z, совпадающую с осью цилиндра, и двумя составляющими будут PHI и Z составляющие H.

В случае tangential H field имеется следующее предостережение: это граничное условие должно быть определено таким образом, чтобы закон полного тока не нарушался в области задачи и на границах.

Граничные условия Symmetry используются, чтобы решить задачи с симметрией и, таким образом, позволить пользователям использовать в своих интересах значительно меньший размер задачи для заданной точности.

Граничные условия Symmetry могут быть двух видов:

• Нечетная (поток тангенциален)

• Четная (поток нормален)

Хотя использование граничных условий симметрии в некоторой степени перекрывается предыдущими условиями, в случаях очевидной симметрии должны использоваться только граничные условия симметрии.