Метод конечных элементов (Finite element method) является очень сложным инструментом, широко используемым инженерами, учеными и исследователями, чтобы решить технические задачи, возникающие в различных физических полях, таких как электромагнитные, тепловые, прочностные, гидродинамические, акустические и др. В настоящее время метод конечных элементов - явно доминирующий численный метод анализа для моделирования распределения физического поля, по успешности не сравнимый с любым другим численным методом. Как правило, метод конечных элементов находит решение любой технической задачи, которая может быть описана конечным набором пространственных уравнений частной производной с определенной границей и начальными условиями. Он используется, чтобы решать задачи в чрезвычайно широком круге технических применений для статических, установившихся и переходных процессов. Метод применяется на разнообразных рынках, таких как автомобильный, космический, ядерноэнергетический, биомедицинский и т.д.
У метода конечных элементов есть твердая теоретическая основа. Она базируется на математических теоремах, которые гарантируют асимптотическое стремление результата расчета поля к точному решению при уменьшении размеров конечных элементов, используемых в процессе решения. Для решений во временной области пространственная дискретизация задачи должна улучшаться совместно с временным шагом расчета, который должен соответствовать предполагаемым временным константам задачи (таким как магнитная диффузионная постоянная времени).
Maxwell решает задачи электромагнитного поля, используя уравнения Максвелла в конечной области пространства с соответствующими граничными условиями и, когда это необходимо, с определенными пользователем начальными условиями, чтобы получить решение с гарантируемой единственностью. Чтобы получить набор алгебраических уравнений, которые будут решены, геометрия задачи автоматически разбивается на четырехгранные элементы (тетраэдры). Все эти объемные объекты модели автоматически объединяются в сетку генератором сетки (mesher). Набор всех тетраэдров называется сеткой конечных элементов модели или просто сеткой. В каждом четырехграннике переменные величины поля для вычисляемой области определяются многочленами второго порядка. Таким образом, в областях с резким пространственным изменением поля плотность сетки должна быть увеличена для хорошей точности решения (см. также adaptive mesh refinement).

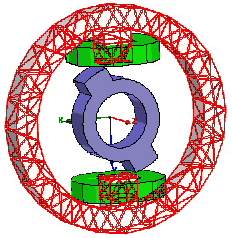
Сетка показана в статоре привода.