|
|
|
Пусть дана катушка без сердечника из Примера 1. Необходимо посчитать её активное сопротивление.
Определить активное сопротивление можно через электрические (омические) потери.
|
| Теория |
Активное сопротивление любого проводника определяется:
где ρ = 1,7∙10-8 Ом∙м – удельная проводимость материала (в данном случае - меди),
l – длина проводника, м,
S – площадь поперечного сечения проводника, м2.
Определим длину проводника. Для этого рассчитаем длину витка и умножим её на число витков. При этом длина витка будет равна длине окружности:
Определим площадь поперечного сечения проводника. В реальности проводник имеет круглое сечение, Maxwell же рассчитывает потери для всей области занятой катушкой, т.е. предполагается, что проводники полностью заполняют область. В случае, если необходим точный расчёт для катушек, намотанных проводом круглого сечения, каждый проводник катушки должен быть прорисован отдельным объектом.
Исходя из вышесказанного, будем условно считать, что катушка намотана проводником прямоугольного сечения. В этом случае площадь поперечного сечения проводника будет определяться:
Определим сопротивление обмотки:
| | Модель |
Построим геометрию модели из Примера 1 в 3D. Для этого нажимаем ПКМ на проекте модели 2D примера 1 и выбираем Create 3D Design. После чего модель будет автоматически преобразована в 3D.
1. Создадим сечение для задания возбуждения катушки.
Для этого выделим объект катушки и применим к нему операцию "сечение" (меню Modeler > Surface > Section, выбираем плоскость сечения YZ). Получим объект, состоящий из двух сечений. Для задания возбуждения необходимо одно сечение, поэтому разделим получившийся объект (меню Modeler > Boolean > Separate Bodyes). Второе сечение не нужно, и его можно удалить.
Последнему сечению назначим величину тока, равную 10 ампер-виткам (ПКМ по сечению > Assign Excitation > Current > Value), тип обмотки – распределённая (Stranded).
2. Задание граничных условий.
В 3D постановке задачи в Maxwell по умолчанию действует условие обнуления поля на границах модели. В отличии от 2D постановки задачи открытых границ (условие Balloon) в 3D нет. Поэтому расчётную область иногда приходится увеличивать до тех пор, пока результат расчёта модели не перестанет ощутимо изменяться.
Создадим область для расчёта: Create Region  (Создание региона), в открывшемся окне выберем Pad Individual Direction и по каждой оси отступим 40% от объектов модели:
Граничные условия для модели не задаём, т.к. действует граничное условие по умолчанию (присваивается нулевая величина поля на границе расчётной модели).
3. Создание сетки элементов и задания на расчёт.
Далее – создаём сетку конечных элементов, предварительно выделив все объекты модели (Assign Mesh Operation > Inside Selection > Length Based… )
Создаём новое задание на расчёт с параметрами по умолчанию (ПКМ на Analysis > Add Solution Setup)
Запускаем задачу на расчёт.
Рисунок П.2.1 – 3D модель рассчитываемой катушки
4. Расчёт омических потерь катушки.
Запустим калькулятор поля (ПКМ на Field Overlays > Calculator…)
В калькуляторе поля (Рисунок П.2.2), необходимо задать следующее выражение:
Рисунок П.2.2 – Калькулятор поля Maxwell
где V – объём, в котором рассчитываются потери (обмотка);
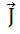 - вектор плотности тока в обмотке;
σ = 1/ρ = 58∙106 См/м – удельная проводимость материала (в данном случае - меди).
Запишем искомое выражение в калькуляторе поля, набрав следующую последовательность команд:
| Quantity > J | Выбираем вектор плотности тока |
| Push | Дублируем |
| Number > Scalar > Value 58000000 | Вводим величину удельной проводимости меди |
| / | Делим плотность тока на проводимость |
| Dot | Перемножаем |
| Geometry > Volume > Coil | Выбираем объём катушки (вместо Coil выбрать название катушки) |
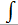 | Интегрируем выражение по объёму. |
В строке выражений получится:
Scl : Integrate(Volume(Coil), Dot(<Jx,Jy,Jz>, /(<Jx,Jy,Jz>, 58000000)))
Получившееся выражение сохраняем в качестве переменной (Named Expression): PowerLoss (кнопка Add..)
Разделим получившиеся потери на квадрат тока ( I = 1 А ) в проводнике (выбираем PowerLoss в списке переменных > Copy to Stack > Eval > Number > Scalar > 1 > / (операция деления).
Получим результат: R = 0,022687 Ом.
Сравним с теоретическим результатом: R = 0,02244 Ом, погрешность составила: 0,1%.
Примечание: Нельзя забывать, что сечение электропроводящего материала в катушках, намотанных проводником круглого сечения, не будет соответствовать реальному сечению катушки. Поэтому нельзя в модели строить сечение катушек по реальным данным, т.к. это приведёт к уменьшению активного сопротивление катушки. В модели сечение катушки должно совпадать с сечением электропроводящего материала (медь, алюминий). Это сечение можно рассчитать, перемножив сечение провода на число витков в катушке.
Автор материалов: Drakon (С) 2014. Редактор: Админ
|
| |
